その２

Table of Contents

その２

やること

関数を書いてみる。

解説

ROOT には関数を扱うクラス（）の TF1, TF2, TF3 があります。関数を書くだけではなく，実験データへのフィッティングにも使います。ちょっと試してみましょう。

１次元（TF1）

TF1 クラスのオブジェクトを作る方法はいくつかありますが，

TF1 (const char *name, const char *formula, Double_t xmin, Double_t xmax, Option_t *option)

という書式をよく使います。ここで

name: このオブジェクトの名前（任意）
formula: 関数を書く (sin(x) など）
xmin: 関数の範囲の下限
xmax: 関数の範囲の上限

です。

例えば

TF1* f = new TF1( "name" , "sin(x)", -3.14, 3.14 );

のように書きます。関数は sin, con のような簡単な数学関数の他に，よく使うものが gaus のような名前で登録されています。代表的なものは

gaus : ガウス関数 \( p_0 \exp \left\{ \frac{-1}{2}\left( \frac{x - p_1}{p_2} \right)^2 \right\} \)
pol1 : 1 次関数 \( p_0 + p_1x \)
poln : n 次関数 \( \sum_{i=0}^{n} p_ix^i \) (n は数字に置き換える)
expo : e の指数関数 \( \exp \left( p_0 + p_1x \right)\)

です。以下のようなこともできます

gaus(0) + gaus(3) + pol1(6)

これは \[ p_0 \exp \frac{-1}{2}\left( \frac{x - p_1}{p_2} \right)^2 + p_3 \exp \frac{-1}{2}\left( \frac{x - p_4}{p_5} \right)^2 + p_6 + p_7x \] という意味です。

詳しくは TFormula を参照してください。

書いてみる

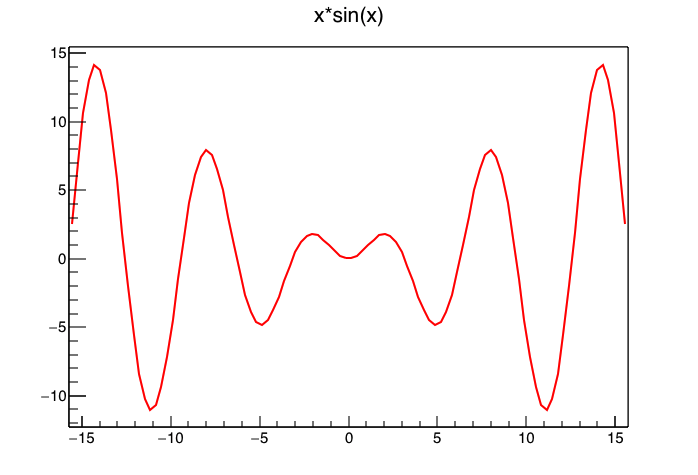
\( x\sin (x) \) を書いてみましょう。対話的に実行してもいいですが，以下のようなマクロファイルを用意するのが便利です。

int macro()
{
    double range_unit = 5.0;
    TF1* f = new TF1( "name" , "x*sin(x)" , -3.14*range_unit , 3.14*range_unit);
    f->Draw();
    return 0;
}

5 行目の “f->Draw();” というのがTF1を描く（C/C++的な意味での）関数です。これを実行すると

\(x \sin (x) の図\\)。 — \(x \sin (x) の図\)。

のようになります。

関数形を少し変え，\( x\sin(x + \theta ) \) を書いてみましょう。関数は

x * sin( x + [0] )

と書きます。 “[0]” が \( \theta \) に対応するパラメータです。このままでは “[0]” の値が設定されていないため，デフォルトで設定されている 0 が代入されて面白くありません。以下のようにして初期値を設定しましょう

f->SetParameter( 0 , 3.14 );

2 つ目の引数でパラメータの番号を指定します。 2 つめの引数でパラメータにセットする数字を与えます。つまりの0 は [0] を意味し，3.14 は [0] に適用される値です。これを実行すると

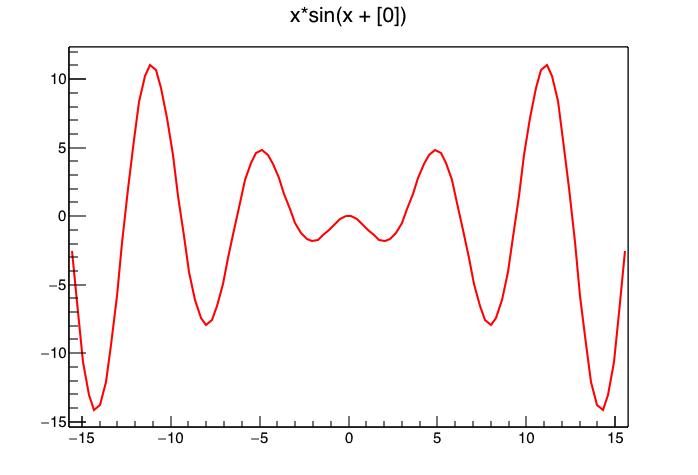
\( x \sin (x+\theta)\\) の図。 — \( x \sin (x+\theta)\) の図。

のように位相が 3.14 ずれます。

見た目を調整してみる

線の色やパターン，太さを変更することができます。例えば

  f->SetLineColor( kBlue ); // 色の変更
  f->SetLineStyle( 2 ); // 線のスタイルの変更
  f->SetLineWidth( 5 ); // 線の太さ変更

をやると以下のようになります。

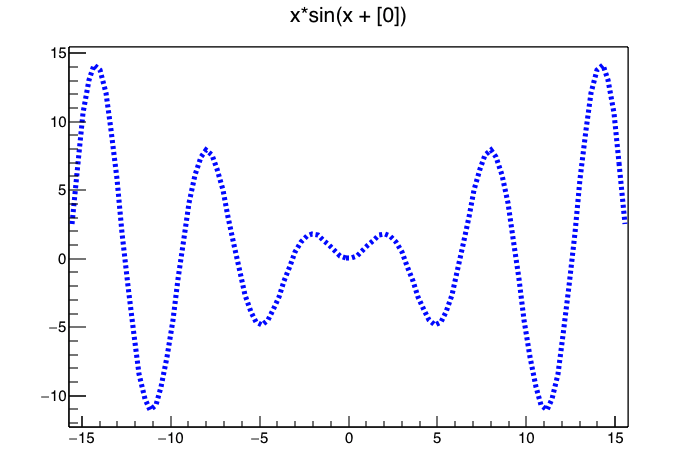
太い青点線で描いた \( x \sin (x) \\) の図。 — 太い青点線で描いた \( x \sin (x) \) の図。

“SetLineColor” 関数は int 型の引数を受け取ります。 1 は黒，2 は赤のように数字と色の対応が決められています。また，あらかじめ kRed, kBlue という変数が定義されているので，それを使うこともできます。線のスタイル，色は TAttLine を参考にしましょう。色は TColor も参考になります。明るい色を使うと見にくくなることが多いようです。

複数の関数を同時に書く

上で \( x\sin(x) \) の位相を変えてみました。面白そうなので，２つの関数を同時に書いてみましょう。

異なる関数を同時に書くには，２つのオブジェクトを作る必要があります。これは異なる数字を同時に保持するために int 型変数を 2 つ作るのと同じようなことです。以下のようなマクロを書いてみました。

int macro()
{
    double range_unit = 5.0;
    TF1* f = new TF1( "name" , "x*sin(x + [0])" , -3.14*range_unit , 3.14*range_unit);
    f->SetLineColor( kBlack );
    f->SetLineStyle( 2 );
    f->SetLineWidth( 2 );

    TF1* f2 = new TF1( "name" , "x*sin(x + [0])" , -3.14*range_unit , 3.14*range_unit);
    f2->SetParameter( 0, 3.14 );
    f2->SetLineColor( kRed );
    f2->SetLineStyle( 1 );
    f2->SetLineWidth( 2 );

    f->Draw();
    f2->Draw( "same" );
    return 0;
}

ポイントは

TF1* f と TF * f2 の２つを作った
f2 を Draw するときに “same” オプションを与えた

です。 “same” オプションをなくすと，f1 を描いたキャンパスが上書きされ，f2 のみが描かれます。上のマクロを実行すると以下のような絵が得られるはずです。

関数からある x における値を得る

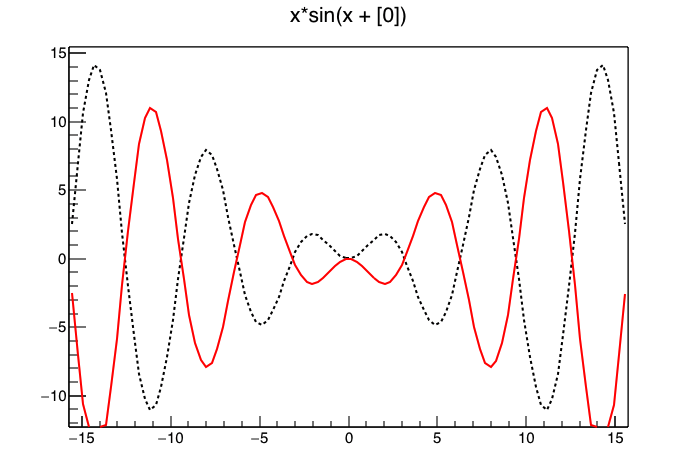
数学関数を使っているのだから，ある x における関数の値を取得したいことがあると思います。そのときは

f->Eval( 3.14 );

のようにします。

２次元 (TF2)

2 次元の関数は TF2 クラスで書きます。 TF1 と似たような使い方で，

int macro()
{
    TF2* f = new TF2("name" , "sin(x) * sin(y)", -10, 10, -10, 10 );
    f->Draw();
    return 0;
}

のようにやると \( \sin (x) \times \sin (y) \) が

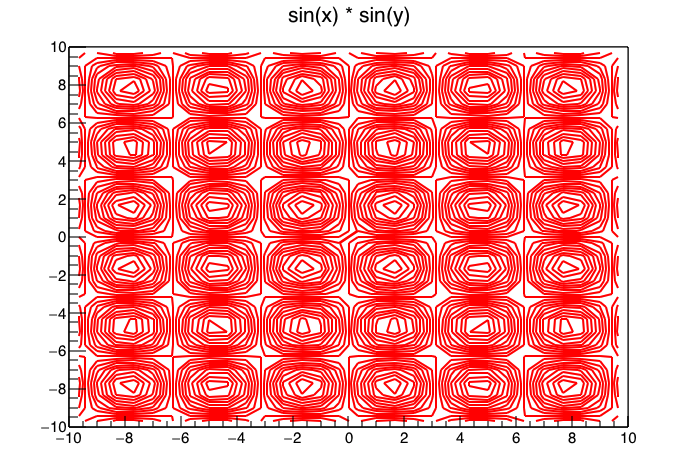
\( \sin(x) \times \sin (y)\\) の図。 — \( \sin(x) \times \sin (y)\) の図。

のように描けます。赤い線が等高線を表していますが，わけがわかりません，

Draw オプションに “colz” を渡し，z 軸を等高線ではなく色の変化で表すと

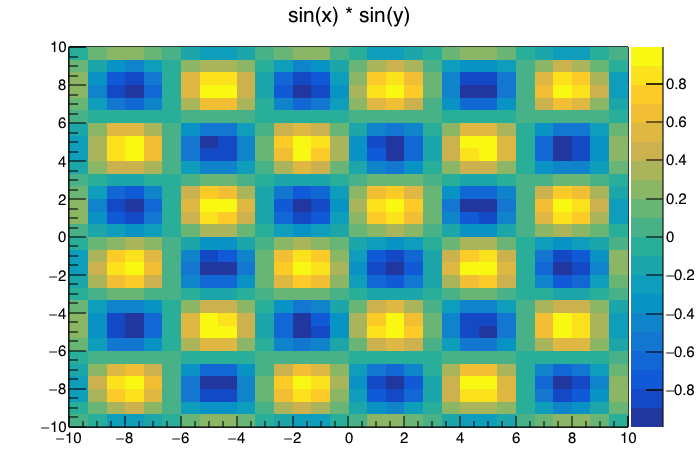
のようになります。ずいぶん見やすくなりました。

3 次元的にも描くことができ，“surf2” オプションを使うと

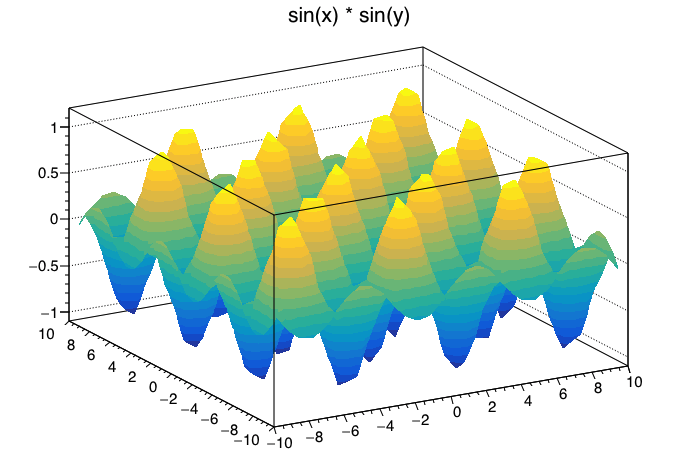
のようになります。

Draw の option は THistPainter を参考にしてください。

関数の書き方

TF1 では gaus や expo などの関数があらかじめ定義されていました。 TF2 でも利用できますが，書き方は少し注意が必要です。

以下は x のガウス関数と y のガウス関数の積 \[ p_0 \exp \left\{ \frac{-1}{2}\left( \frac{x - p_1}{p_2} \right)^2 \right\} \times p_3 \exp \left\{ \frac{-1}{2}\left( \frac{y - p_4}{p_5} \right)^2 \right\} \] です。

TF2* f = new TF2("name" , "gaus(x, [0..2]) * gaus( y , [3..5] )", -10, 10, -10, 10 );   
f->SetParameter( 0, 10 );
f->SetParameter( 1, 0 );
f->SetParameter( 2, 5 );
f->SetParameter( 3, 10 );
f->SetParameter( 4, 0 );
f->SetParameter( 5, 5 );

\( Gaus(x) \times Gaus(y)\\) の図。 — \( Gaus(x) \times Gaus(y)\) の図。

課題

課題１

独立なスピン 1/2 を持つ粒子が外部磁場 \(B\) にさらされると，粒子のスピンは磁場に対して平行 (+) か反平行 (-) の向きになり，エネルギー準位が 2 つに分裂します。各エネルギー準位をとる粒子の数を \(N_+\), \(N_-\) とおくと，熱平衡状態 (TE) のとき \[ N_{\pm} \propto \pm \frac{ \mu B}{k_B T} \] と表されます。ここで \(\mu\) は粒子の磁気モーメント，\(k_B\) はボルツマン定数，\(T\) は系の絶対温度です。

偏極度 \(P\) を

\[ P \equiv \frac{ N_+ - N_-}{N_+ + N_-} \]

と定義すると，TE では

\[ P_{TE} = \tanh \left( \frac{\mu B}{k_B T} \right) \]

となります。粒子の偏極度をを電子・陽子の場合について B の関数で TF1 を用いて書きましょう。また，0.1 K におけるそれぞれの偏極度を求めましょう。

さらに，B, T の関数として TF2 を用いて 2 次元の関数として描いてみましょう。

回答案

回答案をその３で再利用します。