Energy Calibration

はじめに

使用したデータ

BG_HV1850_0615.root
Co60_15cm_HV1850_0615.root
Cs137_20cm_HV1850_0615.root
Na22_30cm_HV1850_0615.root

BG_HV1850_0615.root

K-40(1461keV)に対するfitting

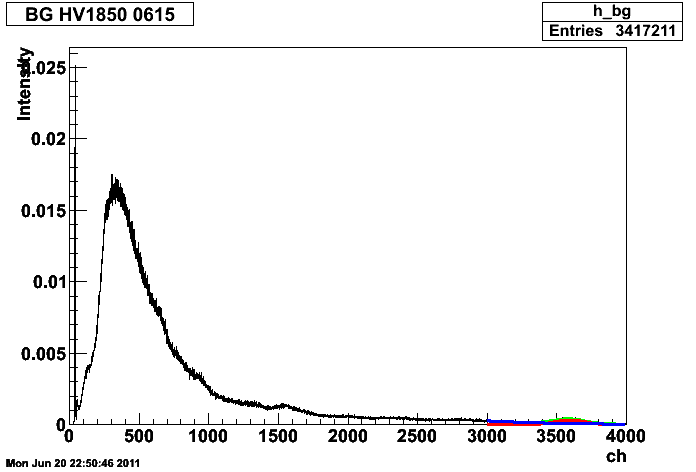
Constant 0.000331432
Mean(ピークの中心) 3591.28[ch]
Sigma(ガウス関数の幅)111.124[ch]
pedestal 39.5402[ch]
という結果でした

Cs137_20cm_HV1850_0615.root

Cs-137(33keV,662keV)に対するfitting

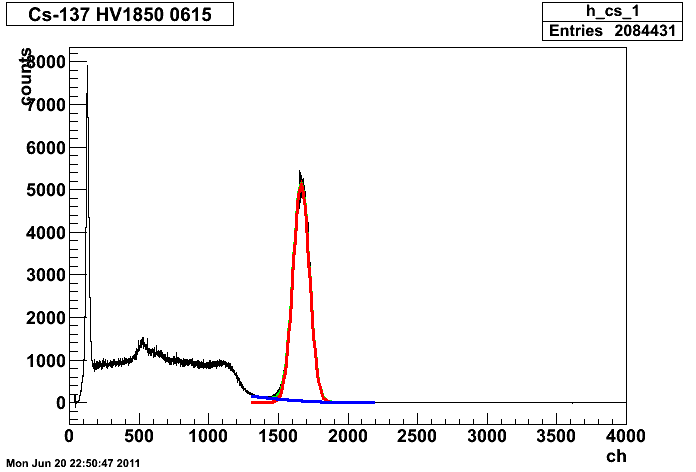
^137mBaによるガンマ線(32.2keVと36.4keV)

Constant 6321.43
Mean(ピークの中心) 128.505[ch]
Sigma(ガウス関数の幅) 12.018[ch]

ガンマ線(662keV)5113.78

Constant 5113.78
Mean(ピークの中心) 1663.79[ch]
Sigma(ガウス関数の幅)58.3712[ch]

という結果でした

Na22_30cm_HV1850_0615.root

Na-22(511keV,1275keV)に対するfitting

ガンマ線(511keV)

Constant 8347.07
Mean(ピークの中心) 1299.28[ch]
Sigma(ガウス関数の幅) 50.191[ch]

ガンマ線(1275keV)

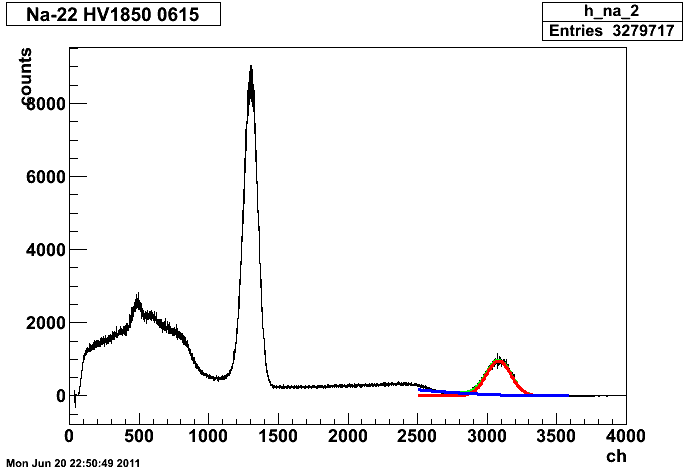
Constant 947.754
Mean(ピークの中心) 3082.53[ch]
Sigma(ガウス関数の幅)89.0246[ch]

という結果でした

Co60_15cm_HV1850_0615.root

Co-60(1173keV,1333keV)に対するfitting

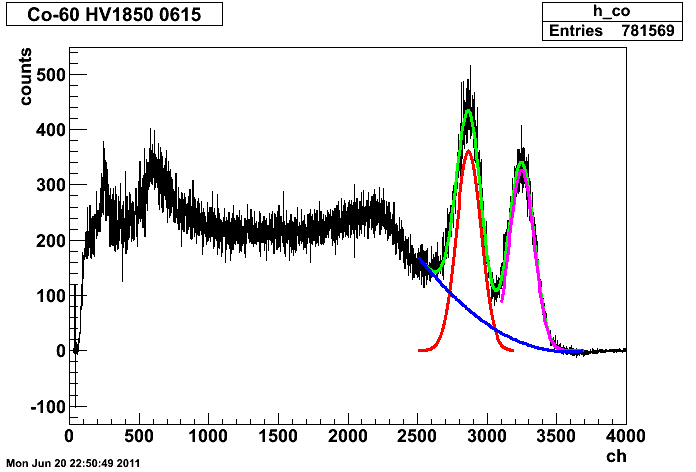
ガンマ線(1173keV)
Constant 360.083
Mean(ピークの中心) 2867.66[ch]
Sigma(ガウス関数の幅) 88.7918[ch]

ガンマ線(1333keV)326.495
Constant 326.495
Mean(ピークの中心) 3248.08[ch]
Sigma(ガウス関数の幅)89.1646[ch]

という結果でした

エネルギーとch

エネルギーとchの対応は
[Energy] = 0.408906 [ch] -16.1682

でした。

sigmaとch

sigmaとchの対応は
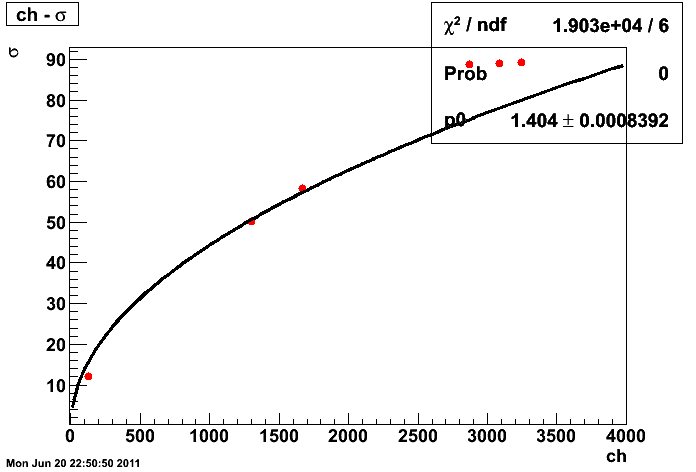
[sigma] = 1.40378*sqrt[ch]

でした。

作業の過程をpdfファイルにまとめるとこうなります。 pdfファイル
最後に、解析に使ったマクロを貼っておきます。全部の作業を一つで終わらせようとしたので非常に汚い。マクロ